ANTI-GRAVITY MIRROR CORNER REFLECTOR SPHERICAL REFLECTIONS
REFLECTIONS
How many of you have gone to a carnival or a circus, paid an admissions fee, and walked through a “Fun Hours?” In these “”Fun Houses” there are ramps, slides, ball pits, levers, and many unusual things. But, what really catches your eye, are those funny looking mirrors. When a person walks by one of these mirrors or up to one, the reflection of the mirror looks distorted and peculiar. If two mirrors are facing directly across from each other, the reflections seem to go on for infinity. What makes these mirrors do these strange things? Why are the reflections the way they are? Today we would like to share with you the answers to these questions. We will be looking at how images are formed when reflected off of a flat mirror, a spherical mirror, and the combination of two or more flat or spherical mirrors.
First of all, we would like to share with you the images formed by a refection in a flat mirror. It works like this: As the rays from an object are reflected by a mirror, the reflected rays appear to come from the mirror. The image is called a virtual image since the rays do not actually passes through or come from the image; they just appear to come from the image. So, if you have a flat mirror, the image reflected back at you is not distorted or changed.
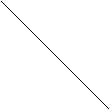
What happens to the light rays though when they hit a flat mirror? To answer this question one needs to know what the angle of incidence is. This is an angle that is made by an incoming light ray and the mirror. Now, the ligh5t ray bounces off the flat mirror so that the angle of incidence is equal to the angle of coincidence, which is the angle, that the outgoing, or reflected, light ray makes with the mirror. So now we know that the angle of incidence is equal to the angle of coincidence. Can this be proven? No matter how many experiments we perform, we can’t be absolutely certain that the “low” like this is always true. Physicists and mathematicians use this “low” though and some trigonometry to calculate the slope of the reflected light ray when an incoming vertical light ray hits a mirror whose slope is m as you can see in Figure 1 below.
The
formula for this is: Slope of outgoing light ray =
Furthermore, we noticed while looking at how a light is reflected from a flat mirror that: if incoming light ray s are parallel to each other, the reflected or outgoing light ray s are also parallel. Therefore you end up with a patter on parallel lines.
So now we know how light is reflected off of a flat mirror, but now what happens when a light ray is reflected off a curved mirror? First, we will look at the image formed by a concave mirror. A concave mirror that is part of a ball or hollow sphere (that is, it has a circular cross section) is a spherical mirror. The focal length is approximately one-half the radius of curvature. A ray that is both parallel and very close to the optical axis will be reflected by the mirror so that it goes through the focal point. A ray striking the mirror at the optical axis is reflected so that the angle of reflection is equal to the angle on incidence. A ray appearing to come from the focal point strikes the mirror and is reflected parallel to the optical axis. This is illustrated below in Figure 2.
The focal point also determines how an object will be reflected. When an object is beyond the focal point of a concave mirror, the image formed will be real and inverted. (A real image can be projected on the screen). If the object is very far away and the light rays are parallel when reaching the surface of the mirror, the image will form at the focal point. If the object emitting the light rays is at the focal point, the reflected rays will not form a real image. Instead, the reflected rays leave the surface of the mirror parallel to one another. Another possibility is if the object is between the focal point and the mirrored surface. In this case, the image will be virtual, larger, and right side up.
Now we will look at the images formed by convex mirrors. The focal point of a
convex mirror is behind the mirror instead of in front of the mirror (opposed to
the concave mirror). Yet the rays are still reflect in three ways but different
from that of the reflection on a concave mirror. First of all, if a ray is
parallel to the optical axis, it is reflected as if it came from the focal
point. A ray directed toward the focal point is reflected parallel to the
optical axis. A ray striking the mirror at the optical axis is reflected at an
angle equal to the angle of incidence (See Figure 3). The images produced by
these convex mirrors are smaller then they would be in a flat mirror and appear
to form behind the mirror.
Figure
3
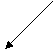
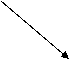
A way to figure out exactly how a ray is reflected off of a curved mirror is by magnifying the small section at the precise point of reflection. First of all, at this point, one must find the slope of the magnified line. You can solve this many different ways, and today we will show you two of those ways.
The first way we will show this to you is by solving the problem geometrically. For example, we will say that the circular mirror has a radius of 8 units and it’s center is at the point (0,8). The (lower half) of this circle can be described by the equation y=f(x) where f(x) is the function: f(x) = 8- 64-x2 Next, we must find the slope of the line
between the two point (0,8) and (x, 8- 64-x2 ). So, the slope of this line (L) is equal to
This line then can be used to find the slope of the tangent, because this line and the tangent line meet at right angles. Therefore, the slope of the tangent is the negative reciprocal of the slope of the line (L) which equals:
We can approach this same problem algebraically too. This can be done by finding the derivative of the function f(x). The process of doing this is as follows:
Notice that by solving geometrically and solving algebraically the two final equations agree with each other. Now that we have found the slope of the line, one can measure the angle of incidence between the slope of the line and the incoming ray and therefore determine the angle of coincidence.
The next question for us to answer is: what kinds of reflections occur when there is a combination of two or more flat mirrors? An image is formed each time the light bounces off a mirror. The number of images that you see in the mirrors depends on the angle that the mirrors form. As you make the angle between the mirrors smaller, the light bounces back and forth more times, and you see more images. There is a rule that determines how many images are seen based on a certain angle. This rule is: 360 divided by the angle between the mirrors gives the number of images, plus one. For example, 360/90 = 4, so you should see three images of the object. 360/60 = 6, so you should see five images of the object and so on. If two mirrors are parallel to each other, the images will go on for infinity.
When three mirrors meet, this is called a corner reflector. (Link to corner reflector web page for more information). Rays of light that are pointed at the corner will bounce from mirror to mirror and then exit parallel to the entering ray. Light from the center of you eye bounces straight back to the center of your eye, so the image of your eye seems to be centered in the corner made by the mirrors. Additionally, in a corner reflector, multiple reflections reverse the image and invert it.
Now what happens when spherical mirrors reflect with each other? This can be described most sufficiently by creating a set of spherical reflections using Christmas tree balls. Each sphere reflects its six neighbors, along with their reflections. The result of this is that the balls appear to be shiny hexagons with black triangular spaces between them. Also when you look at the set of Christmas tree balls, the image of your eye is at the center of every sphere. If you point your finger at one sphere, the finger’s image in all the others spheres will point directly at the chosen sphere. This is all due to the spherical symmetry of reflectors which is explained more in depth on the link to “Christmas Tree Balls”.
So, we know we know how images are formed when reflected off of a flat mirror, a spherical mirror, and the combination of two or more flat or spherical mirrors. This knowledge does not only answer the questions for the mirrors used in “Fun House” though. This understanding of reflections has been useful in the use and design of many things. Flat mirrors are used for multiple purposes such as architectural design, interior decorating, and the basic use as a viewing instrument for cosmetic and medicinal purposes. Convex and concave mirrors are used as reflectors in flashlights, some telescopes, solar ovens, as rear-view reflectors on cars, and essentially the concept of a concave mirror was used to invent satellites. The understanding of the reflections of flat mirrors, spherical mirrors, and the combination of two or more flat or spherical mirrors has proven to be very useful in many of our everyday items that we use and enhance our lives. Hopefully, society will continue to use this knowledge and understanding of the reflection of mirrors to their benefit.
Bibliography
Colwell, Catharine H. “Physics Lab Outreach” (1997-2002): On-line. Internet. 19 December 2002. Available WWW: http://online.cctt.org/curriculumguide/units/reflection.asp
Dzrieba, Alex R. “Physical Optics” On-line. Internet. 22 December 2002. Available WWW: http://dustbunny.physics.indiana.edu/~dzierba/P360n/notes/note3.pdf
“Laws of Reflection” (5 October 1993) On-line. Internet. 26 December 2002. Available. WWW: http://unite.ukans.edu/explorer/explorer-db.html
“Optics, An educators guide in science and mathematics” On-line. Internet 22 December 2002. Available WWW: http://teacherlink.ed.usu.edu/tlnasa/units/Optics/10Activity04.pdf
“Reflection of light in mirrors” (9 December 2002) On-line. Internet. 21 December 2002. Available. WWW: http://resources.mhs.vic.edu.au/science/year9resources/ray_diagrams_mirrors.htm
“Reflection of Mirrors” On-line. Internet. 26 December 2002. Available
WWW: http://www.glencoe.com/sec/science/lep_science/lep2002.pdf
“The Science of Light” On-line. Internet. 26 December 2002. Available. WWW: http://www.learner.org/teacherslab/science/light/lawslight/funhouse/funhousebackground.html
“2002 The Exploratory” On-line. Internet. 26 December 2002. Available WWW: http://www.exploratory.org.uk/exhibits/mirrors.htm Vulcan, Douglas.